Empirically Measuring Concentration
Estimating the Intrinsic Robustness for Image Benchmarks
Recent theoretical results, starting with Gilmer et al.‘s Adversarial Spheres (2018), show that if inputs are drawn from a concentrated metric probability space, then adversarial examples with small perturbation are inevitable.c The key insight from this line of research is that concentration of measure gives lower bound on adversarial risk for a large collection of classifiers (e.g. imperfect classifiers with risk at least $\alpha$), which further implies the impossibility results for robust learning against adversarial examples.
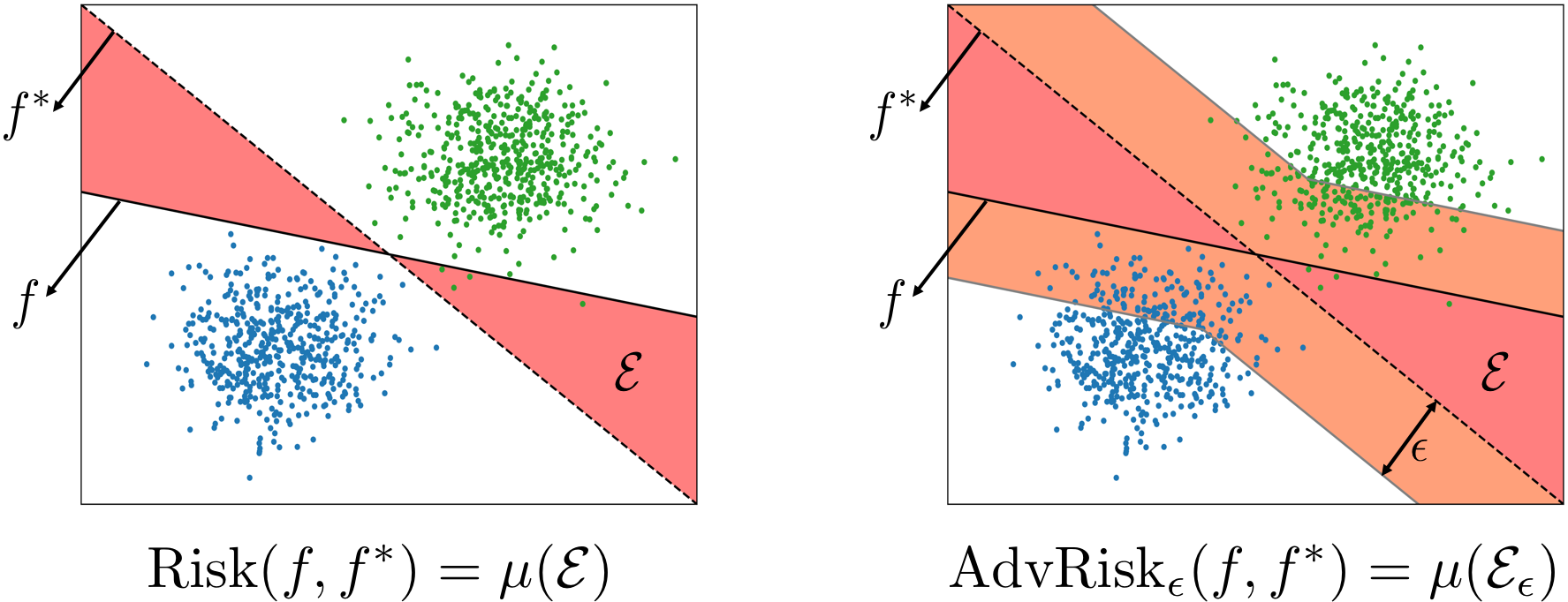
However, it is not clear whether these theoretical results apply to actual distributions such as images. This work presents a method for empirically measuring and bounding the concentration of a concrete dataset which is proven to converge to the actual concentration. More specifically, we prove that by simultaneously increasing the sample size and a complexity parameter of the selected collection of subsets $\mathcal{G}$, the concentration of the empirical measure based on samples converges to the actual concentration asymptotically.

To solve the empirical concentration problem, we propose heuristic algorithms to find error regions with small expansion under both $\ell_\infty$ and $\ell_2$ metrics.
For instance, our algorithm for $\ell_\infty$ starts by sorting the dataset based on the empirical density estimated using k-nearest neighbor, and then obtains $T$ rectangular data clusters by performing k-means clustering on the top-$q$ densest images. After expanding each of the rectangles by $\epsilon$, the error region $\mathcal{E}$ is then specified as the complement of the expanded rectangles (the reddish region in the following figure). Finally, we search for the best error region by tuning the number of rectangles $T$ and the initial coverage percentile $q$.
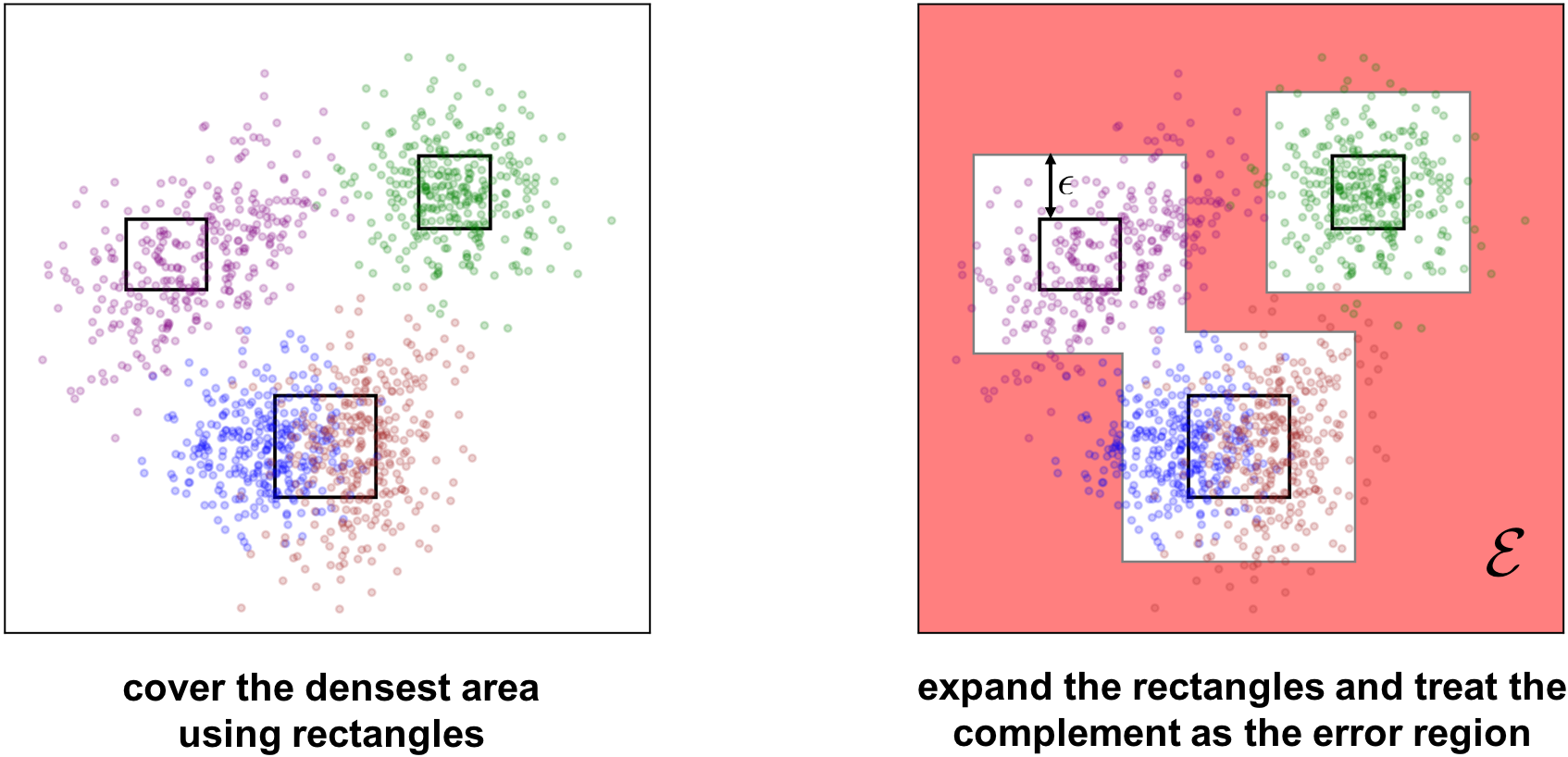
Based on the proposed algorithm, we empirically measure the concentration for image benchmarks, such as MNIST and CIFAR-10. Compared with state-of-the-art robustly trained models, our estimated bound shows that, for most settings, there exists a large gap between the robust error achieved by the best current models and the theoretical limits implied by concentration.

This suggests the concentration of measure is not the only reason behind the vulnerability of existing classifiers to adversarial perturbations. Thus, either there is room for improving the robustness of image classifiers or a need for deeper understanding of the reasons for the gap between intrinsic robustness and the actual robustness achieved by robust models.
Papers
Jack Prescott, Xiao Zhang, and David Evans. Improved Estimation of Concentration Under ℓp-Norm Distance Metrics Using Half Spaces. In Ninth International Conference on Learning Representations (ICLR). May 2021. [arXiv, Open Review] [Code]
Saeed Mahloujifar★, Xiao Zhang★, Mohamood Mahmoody and David Evans. Empirically Measuring Concentration: Fundamental Limits on Intrinsic Robustness. In NeurIPS 2019 (spotlight presentation). Vancouver, December 2019. [PDF] [arXiv]
Preliminary version presented at Safe Machine Learning and Debugging ML Models workshops at ICLR 2019, as well as Uncertainty & Robustness in Deep Learning workshop at ICML 2019.